Формулою Сімпсона називається
інтеграл від
інтерполяційного многочлена другого
степеня на відрізку
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
:

де
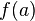
,

і

— значення
функції у відповідних точках .
[ред.] Похибка
При умові, що функція

на відрізку
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
має
похідну четвертого порядку, похибка

, дорівнює:
![E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}, \ \ \ \zeta \in [a,b].](http://upload.wikimedia.org/math/e/4/9/e49ee7873cd9c01c2e7e7d781d863728.png)
Зважаючи, що значення
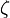
переважно не є відомим, для оцінки похибки використовується нерівність:
![\left| E(f) \right| \le \frac{(b-a)^5}{2880} \max\limits_{x\in[a,b]} {\left| f^{(4)}(x) \right|}.](http://upload.wikimedia.org/math/1/a/7/1a70162208434c2976edef3b381de0bc.png)
[ред.] Виведення формули
Формула Сімпсона може бути виведена за допомогою багатьох різних способів.
[ред.] Квадратична інтерполяція
Якщо замінити функцію

квадратичним поліномом
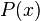
що приймає ті ж значення що й

у точках
a,
b і
m = (
a+
b) / 2. використавши
інтерполяційну формулу Лагранжа, то одержимо формулу:

Після необхідних обчислень одержуємо:
![\int_{a}^{b} P(x) \, dx =\frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right].](http://upload.wikimedia.org/math/1/1/5/115da26758258fe2602edd2aa726f609.png)
[ред.] Використання методів прямокутників і трапецій
У цьому способі виведення використовуються
метод прямокутників:

і
метод трапецій:

Похибки цих наближень дорівнюють
 і
і
відповідно. Звідси випливає, що аби позбутися третього степеня слід взяти для наближення величину

Однак таким чином одержується формула Сімпсона.
[ред.] Метод невизначених коефіцієнтів
Запишемо в загальному виді:

Коефіцієнти α, β і γ можуть бути знайдені з вимоги, що дане наближення є точним для всіх многочленів другого степеня. Таким чином знову ж одержується метод Сімпсона.
[ред.] Ітераційна формула
Для точнішого обчислення інтеграла проміжок
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
розбивають на

відрізків однакової довжини і застосовують формулу Сімпсона на кожному з них. Значення інтеграла є сумою для всіх відрізків.

- де
 величина кроку, а
величина кроку, а  межі відрізків.
межі відрізків.
Загальну похибку

при інтегруванні на відрізку
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
з кроком

визначають за формулою:
![\left| E(f) \right| \le \frac{(b-a)}{2880}h^4 \max\limits_{x\in[a,b]} |f^{(4)} (x)|](http://upload.wikimedia.org/math/1/9/0/1905bd6398a191245afb5e7163ecf8c5.png) .
.
При неможливості оцінити похибку за допомогою четвертої похідної можна використати слабшу оцінку:
![\left| E(f) \right| \le \frac{(b-a)}{288}h^3 \max\limits_{x\in[a,b]} |f^{(3)} (x)|](http://upload.wikimedia.org/math/0/3/7/037bff16fae3bafccbe5d3cfef5c770c.png)
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: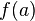 ,
,  і
і  — значення функції у відповідних точках .
— значення функції у відповідних точках . на відрізку
на відрізку ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) має похідну четвертого порядку, похибка
має похідну четвертого порядку, похибка  , дорівнює:
, дорівнює: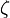 переважно не є відомим, для оцінки похибки використовується нерівність:
переважно не є відомим, для оцінки похибки використовується нерівність: квадратичним поліномом
квадратичним поліномом 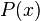 що приймає ті ж значення що й
що приймає ті ж значення що й  у точках a,b і m = (a+b) / 2. використавши інтерполяційну формулу Лагранжа, то одержимо формулу:
у точках a,b і m = (a+b) / 2. використавши інтерполяційну формулу Лагранжа, то одержимо формулу: і
і
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) розбивають на
розбивають на  відрізків однакової довжини і застосовують формулу Сімпсона на кожному з них. Значення інтеграла є сумою для всіх відрізків.
відрізків однакової довжини і застосовують формулу Сімпсона на кожному з них. Значення інтеграла є сумою для всіх відрізків. величина кроку, а
величина кроку, а  межі відрізків.
межі відрізків. при інтегруванні на відрізку
при інтегруванні на відрізку ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) з кроком
з кроком  визначають за формулою:
визначають за формулою:![\left| E(f) \right| \le \frac{(b-a)}{2880}h^4 \max\limits_{x\in[a,b]} |f^{(4)} (x)|](http://upload.wikimedia.org/math/1/9/0/1905bd6398a191245afb5e7163ecf8c5.png) .
.
![E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}, \ \ \ \zeta \in [a,b].](http://upload.wikimedia.org/math/e/4/9/e49ee7873cd9c01c2e7e7d781d863728.png)
![\left| E(f) \right| \le \frac{(b-a)^5}{2880} \max\limits_{x\in[a,b]} {\left| f^{(4)}(x) \right|}.](http://upload.wikimedia.org/math/1/a/7/1a70162208434c2976edef3b381de0bc.png)

![\int_{a}^{b} P(x) \, dx =\frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right].](http://upload.wikimedia.org/math/1/1/5/115da26758258fe2602edd2aa726f609.png)





![\left| E(f) \right| \le \frac{(b-a)}{288}h^3 \max\limits_{x\in[a,b]} |f^{(3)} (x)|](http://upload.wikimedia.org/math/0/3/7/037bff16fae3bafccbe5d3cfef5c770c.png)
Немає коментарів:
Дописати коментар